정현파(sinusoids)의 의미
정현파는 신호의 해석과 처리에서 매우 중요한 역할을 하는 기본적인 신호이다. 정현파는 아래 그림과 같이 길이가 <$A$>인 실에 매달려 반시계 방향으로 각속도 <$\omega$>를 가지고 <$T$>초 마다 한 바퀴씩 등속회전운동을 하는 송의 위치 <$x(t)$>를 시간에 대해 그려 얻는다. 이렇게 신호의 시간에 따른 값의 변화를 나타낸 것을 신호의 파형이라고 하는데, 공이 한 바퀴씩 돌 때마다 <$x(t)$>는 같은 파형을 반복하게 된다.
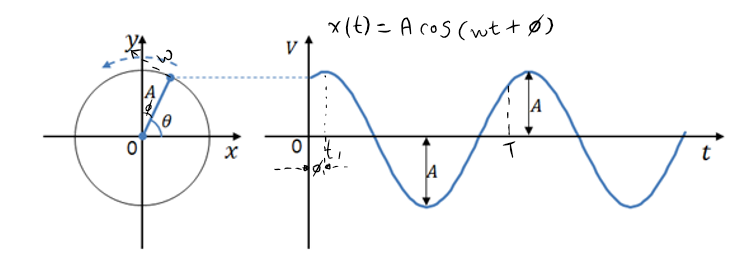
- <$A$>: 진폭amplitude
정현파가 진동하여 가질 수 있는 값의 범위 - <$\phi$>: 위상phase
각으로 표시된 원점에서 코사인파의 꼭짓점(사인파의 0점)까지의 거리 - <$\omega$>: 각주파수radian frequency
정현파가 1초에 이동할 수 있는 라디안 각
$$\omega = {{2\pi} \over {T}} = 2\pi f$$ - <$T$>: (기본) 주기 (fundamental) period
정현파가 같은 파형을 반복하는 (최소)시간 간격
$$T = {{2\pi} \over {\omega}} = {1 \over f}$$ - <$f$>: 주파수 frequency
정현파가 1초에 같은 파형을 반복하는 횟수(진동횟수)
$$f = {1 \over T} = {{\omega} \over {2 \pi}}$$
신호의 표현과 주파수
햇빛과 프리즘의 예는 다음과 같은 중요한 결론을 담고있다.
- 신호를 더 기본적인 신호들로 쪼갤 수 있다는 것
- 신호를 시간이 아닌 주파수의 관점에서 살펴보는 것이 매우 유용하다는 것
[그림 5-1]의 두 신호는 모두 주기가 <$T=1$> 인 주기 신호이다. 하지만 주기가 같다고 해서 주파수 특성이 같다고 말할 수 없다. 왜냐하면 [그림 5-1(b)]의 신호가 [그림 5-1(a)]의 사인파에 비해 값이 빠르게 변하기 때문이다.
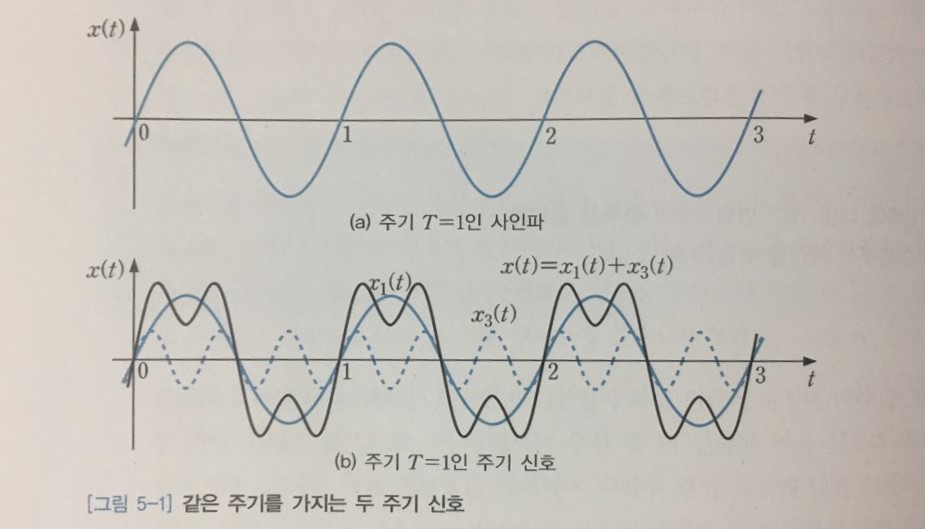
[그림 5-1(b)]의 신호는 그림에 나타낸 것과 같이 주파수가 1Hz와 3Hz인 두 개의 사인파로 이루어진 신호이다. 그러나 신호의 파형만 보고 이를 알아내는 것은 불가능하므로 햇빛을 나누는 프리즘과 같은 역할을 해 줄 도구가 필요하다.
[그림 5-1]에서는 [그림 5-1(b)]의 신호를 두 개의 정현파로 쪼갰지만, 정현파가 아닌 다른 형태의 신호를 기본 신호로 사용함수도 있을 것이다. 그렇다면 기본 신호로 어떤 신호를 사용하는 것이 좋을까? 다음과 같은 성질을 만족하는 신호를(빛이나 색의 삼원색과 같은 역할을 하는) 기본 신호로 선택한다면 여러 가지로 편리하다. 이러한 기본 신호를 수학에서는 기저basis라고 한다.
- 형태가 단순하고, 신호의 표현을 구하기 쉬워야 한다.
- 다양하고 폭넓은 신호들을 표현할 수 있어야 한다.
- 표현된 신호에 대한 시스템의 응답을 편리하게 표기할 수 있어야 한다.
- 한 주파수에 대해 오직 하나의 기본 신호만 존재(일대일대응) 해야 한다.
기본 신호 <$\{ \psi _i (t) \}$>가 선정되면, 식 (5.1)과 같이 이들의 일차 결합으로 신호를 나타낼 수 있으며, 신호의 표현을 구하는 문제는 결국 계수 <$c_i$>를 구하는 문제가 된다.
$$x(t) = \sum_{i} c_i \psi _i (t) \qquad \cdots \ (5.1)$$
정현파는 좋은 기본 신호가 갖추어야 할 성질들을 모두 만족하는 최적의 신호로서, 이 장에서는 정현파를 이용하여 주파수의 관점에서 신호를 표현하고 해석하는 문제를 다루게 된다. 이때 햇빛에 대한 프리즘의 역할을 푸리에 급수와 변환이 맡으므로, 이를 신호의 푸리에 해석이라고도 한다.
모든 정현파는 파형의 모양이 같으므로 서로 구별할 수 있는 정보는 <$t=0$>에서 한 주기의 파형이 어느 위치에서 출발해서(위상 <$\phi$>) 얼마만한 크기로(진폭 <$A$>) 얼마나 빨리 반복되는지(주파수 <$f_0$>)에 관한 것 뿐이다. 따라서 이를 나타내면 다음과 같이 된다.
$$x(t) = Acos(s\pi f0 t + \phi) = Acos(\omega _0 t + \phi) \qquad \cdots \ (5.2)$$
그러므로 정현파를 시간의 함수로 파악하여 시간축 상의 그래프로 나타내기보다 주파수의 함수로 취급하여 주파수축 상에서 진폭과 위상으로 나타내는 것이 훨씬 효과적으로 정보를 전달할 수 있다. 이것이 바로 (주파수) 스펙트럼이며, 신호의 주파수 해석에서 가장 기본이 되는 핵심 개념이다.
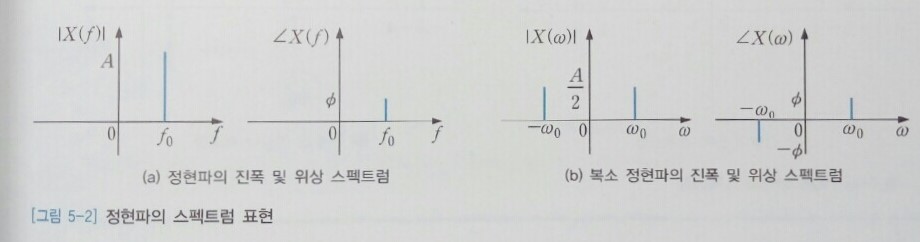
[그림 5-2]는 정현파의 스펙트럼을 나타낸 것이다. 식 (5.2)의 진폭과 위상을 [그림 5-2(a)]와 같이 바로 그릴수도 있지만, 오일러Euler 공식을 이용하여 정현파를 식 (5.3)과 같이 복소 정현파로 바꾸어 표현하고 [그림 5-2(b)]처럼 이것의 진폭과 위상을 그리는 것이 더 일반적이다. 주파수축은 그림에서 보듯이 <$f$>Hz나 <$\omega$>rad/sec 어느쪽을 사용해도 상관없다.
$$x(t) = {A \over 2}e^{j\phi}e^{j2\pi f_0 t} + {A \over 2}e^{-j\phi}e^{-j2\pi f_0 t} \qquad \cdots \ (5.3)$$
푸리에 급수
정현파를 이용하여 신호의 표현을 찾는 문제는 프랑스의 수학자 푸리에가 주기 신호를 주파수가 서로 다른 정현파의 합으로 나타낼 수 있음을 처음 발견한 것에서부터 시작되었다. 따라서 이를 일컬어 푸리에 해석Fourier analysis이라고 한다.
주기 신호와 푸리에 급수
정현파를 기본 신호로 채택하여 주파수에 대한 신호 표현을 찾아내는 문제를 다룰 때, 같은 파형이 규칙적으로 반복되는 주기 신호가 무질서한 신호보다 다루기가 쉬우므로 우선적인 대상이 될 것이다.
푸리에의 결과에 따르면, 주기신호는 그 신호와 같은 주기를 갖는 정현파와 이 정현파의 정수배의 주파수를 갖는 정현파들의 합으로 표현할 수 있다. 이때 주기 신호와 주기(<$T$>)가 같은 정현파를 기본파fundamental wave라 하고, 이 정현파의 주파수 <$f_0 = {1 \over T} \left \{ \omega_0 = {2\pi \over T} \right \}$>를 기본 주파수fundamental period 라 한다. 또한 <$kf_0 (k\omega _0, \ k=2,3,4,\ \cdots \ )$>의 주파수를 갖는 정현파를 <$k$>고조파harmonics 라고 한다.
[그림 5-1(b)]나 [그림 5-3]과 같이 몇 개의 정현파의 합으로 표현되는 주기 신호도 있지만, 보통은 더 많은 수, 경우에 따라서는 무한개의 정현파가 필요한 주기 신호도 있다. 따라서 푸리에의 결과를 일반화하여 수식으로 나타내면 다음과 같은 급수의 형태가 되며, 이렇게 정현파를 이용한 주기 신호의 표현을 푸리에 급수(FS) Fourier Series 라고 한다.
$$x(t) = 직류(DC) + 기본파(cos항 + sin항) + 고조파들(cos항 + sin항) \\ \qquad a_0 + \sum_{k=1}^{\infty}a_k cos k\omega _0 t + \sum_{k=1}^{\infty}b_k sin \omega _0 t \qquad \ \cdots \ (5.4)$$
[기본파, 고조파, 푸리에 급수]
- 기본파: 주기 신호와 같은 주기를 갖는 정현파
- 고조파: 기본파의 주파수(기본주파수)의 정수배 주파수를 갖는 정현파
- 푸리에 급수: 주기 신호를 기본파와 고조파들의 합으로 나타낸 것
주기 신호를 식 (5.4)와 같이 표현하려면 푸리에 계수라고 하는 각 항의 계수 <$a_0 , \ a_k , \ b_k$>를 구해야 하는데, 정현파 신호의 직교성을 이용하면 다음과 같이 쉽게 구할 수 있다.
$$a_0 = {1 \over T}\int_{T} x(t)\ dt \qquad \cdots \ (5.5)$$
$$a_k = {2 \over T}\int_{T} x(t)cosk\omega _0 t\ dt \qquad \cdots \ (5.6)$$
$$b_k = {2 \over T}_{T}x(t)sink \omega_0 t \ dt \qquad \cdots \ (5.7)$$
푸리에 급수의 세 가지 표현
생략
| 형식 | 푸리에 급수 | 계수 계산 | 변환 공식 |
|---|---|---|---|
| 삼각함수 | $$x(t) = a_0 + \sum_{k=1}^{\infty}a_k cosk\omega _0 t \\ \qquad + \sum_{k=1}^{\infty}b_k sink\omega _0 t$$ |
$$a_0 = {1 \over T}\int_{T} x(t)dt$$ $$a_k = {2 \over T}\int_{T} x(t)cosk\omega _0 tdt$$ $$b_k = {2 \over T}_{T}x(t)sink \omega_0 t dt$$ |
$$a_0 = c_0 = X_0$$ $$a_k = c_k cos\phi _k$$ $$b_k = -c_k sin\phi_k = j(X_k - x_{-k})$$ |
| 간결형 삼각함수 |
$$x(t) = \sum_{k=0}^{\infty}c_k cos(k\omega _0 + \phi _k)$$ |
$$c_0 = a_0 ,\ \phi _0 = 0$$ $$c_k = \sqrt{a_k^2 + b_k^2}$$ $$\phi_k = -tan^{-1} \left ({b_k \over a_k} \right )$$ |
$$c_0 = X_0$$ $$c_k = 2|X_k |$$ $$\phi_k = \angle X_k$$ |
| 지수함수 | $$x(t) = \sum_{k=-\infty}^{\infty}X_k e^{jk\omega _0 t}$$ | $$X_k = {1 \over T}\int_T x(t) e^{jk\omega_0 t}\ dt$$ |
$$X_0 = a_0 = c_0$$ $$X_k = {c_k \over 2}e^{j\phi k} = {1 \over 2}(a_k - jb_k )$$ $$X_{-k} = X_k^*$$ |
푸리에 급수는 주기 신호가 기본 주파수의 정수배가 되는 주파수 성분만 가진다는 중요한 사실을 알려준다.
이러한 푸리에 급수 표현이 성립하기 위해서는 푸리에 급수가 수렴해야 하며, 수렴에 관한 조건을 정리한 것이 다음의 디리클레Dirichlet 조건이다.
- 신호의 한 주기 내에서 <$x(t)$>는 절대 적분가능absolutely integrable해야 한다.
$$\int_{T}|x(t)|\ dt$$ - 신호의 한 주기 내에 존재하는 극대 극소점의 수는 유한해야 한다.
- 신호의 한 주기 내에 존재하는 불연속점의 수는 유한해야 한다.
[진폭 스펙트럼의 역할]
진폭 스펙트럼은 힌소가 갖는 다양한 주파수 성분의 양(정현파의 진폭)을 나타낸다. 진폭 스펙트럼은 일반적으로 저주파에서 고주파로 갈 수록 값이 감쇠하는 양상을 보인다. 그리고 파형의 시간적 변화가 완만한 신호는 진폭 스펙트럼의 감쇠가 급격하고, 반대로 시간적으로 급격한 변화를 보이는 신호는 진폭스펙트럼의 감쇠가 완만하다.
파형 변화가 급하지 않고 비교적 매끄러운 신호라면, 신호의 대략적인 모양을 만들어주는 몇 개의 두드러진 저주파수 정현파와 세부적인 변화를 맞추어주는 작은 값의 고주파수 정현파들만으로 신호를 만들 수 있다. 이때문에 진폭 스펙트럼은 주파수 증가에 따라 빠르게 감쇠한다. 따라서 적은 수의 푸리에 급수 항으로도 양호하게 근사적으로 합성할 수 있다. 극단적인 예로 정현파의 경우에는 기본 주파수 <$\omega_0$>에서만 진폭 스펙트럼의 값이 나타난다. 반면에, 불연속점을 갖는 사각 펄스와 같이 급격한 변화를 포함하는 신호는 이를 구현하기 위해 많은 주파수 성분이 필요할 뿐 아니라 고주파 성분의 크기도 상대적으로 무시할 수 없는 값을 갖는다. 따라서 진폭 스펙터름은 주파수에 따라서 느리게 감쇠할 것이고, 신호를 근사적으로 합성할 때 오차를 작게 하려면 많은 수의 푸리에 급수 항이 필요하다.
사각 펄스 신호는 푸리에 급수로 전개하면 무한개의 주파수 성분을 가진다. [그림 5-10]은 스펙트럼에 존재하는 고조파들을 차례로 더하여 사각 펄스 신호를 합성하는 과정을 보인 것이다. 그림에서 보면 세 개의 고조파만 더해져도 사각 펄스와 비슷한 모양을 갖추지만, 아직 불연속점의 날카로운 모서리가 이 합성 신호에는 나타나지 않는다. 왜냐하면 날카로운 모서리를 구현하기 위해서는 급격히 변하는 (고주파수)성분이 필요하기 때문이다. 고조파의 수를 점진적으로 늘림에 따라 모서리는 서서히 날카로워지며 신호는 사각 펄스에 더욱 가까워진다.
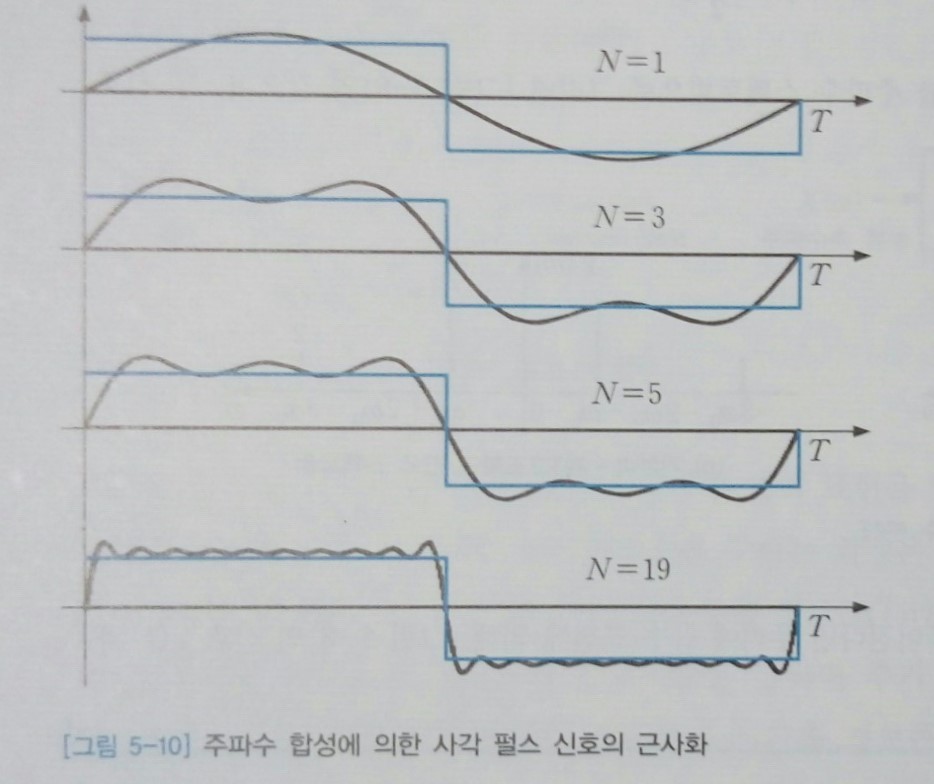
그런데 [그림 5-10]에서 고조파의 수를 늘려가도 불연속점 부근에서 오버슈트가 생기며 파형이 평탄하지 않고 진동하는 현상을 관찰할 수 있다. 이론적으로는 무한개의 고조파를 더하면 정확히 사각펄스가 되어야 하지만, 실제 조파 합성 신호는 고조파의 수를 아무리 늘리더라도 불연속점 근처에서 항상 불연속 크기의 약 9%의 오버슈트가 생기며, 고조파수에 비례하여 진동도 더 빨라진다. 이러한 현상을 깁스Gibbs 현상이라고 한다.
[위상스펙트럼의 역할]
위상스펙트럼은 각 주파수 성분의 시간축 상의 위치를 표시한다. 그러므로 진폭 스펙트럼이 같더라도 위상 스펙트럼이 다르면 신호의 파형이 달라진다. 이에 대한 예를 [그림 5-11]에 나타냈다.
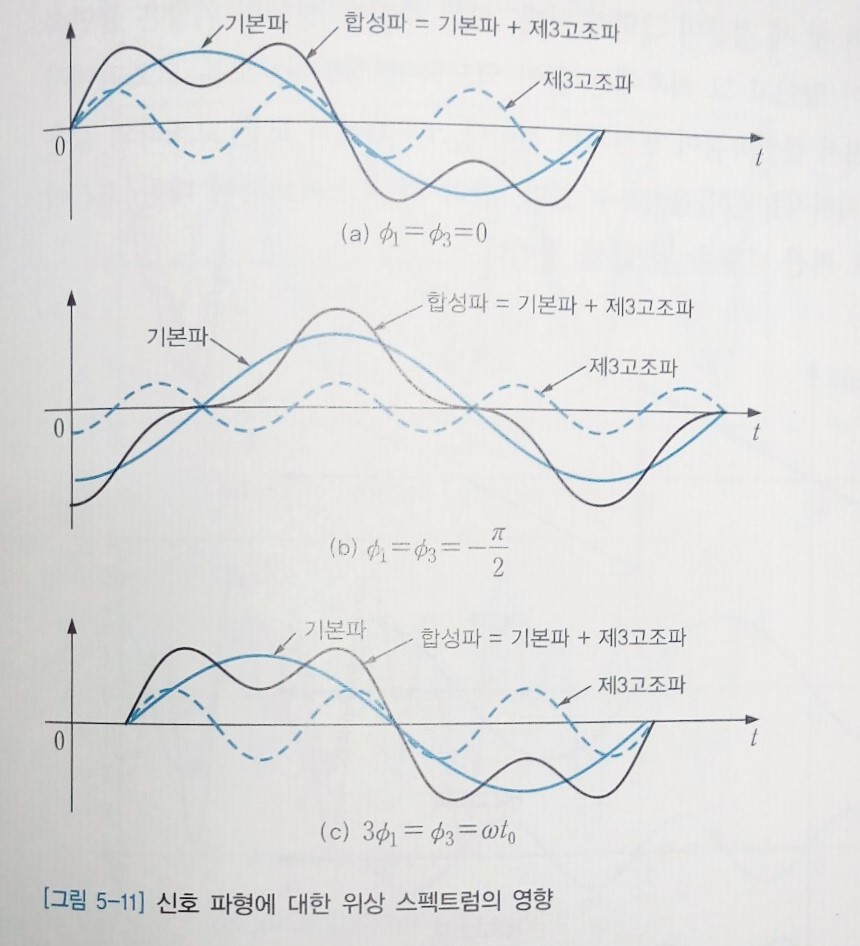
[그림 5-11]의 신호는 모두 기본파와 제3고조파가 더해져서 만들어진 것으로, 진폭은 동일하나 위상이 다른 경우이다. [그림 5-11(a)]는 기본파와 고조파의 위상이 <$\phi_1 = \phi_3 = 0$>인 신호이고 [그림 5-11(b)]는 <$\phi_1 = \phi_3 = - {\pi \over 2}$>로 합성된 신호로서 파형이 완전히 다르다.
그렇다면 두 정현파의 위상 <$\phi_1$>와 <$\phi_3$>사이에 어떤 관계가 있으면 원래의 파형 [그림 5-11(a)]가 유지될 수 있을까? 그림에서 보면 기본파와 제3고조파가 시간축 상에서 똑같은 거리만큼 이동한다면 신호의 파형은 바뀌지 않을 것이며, 이를 나타낸 것이 [그림 5-11(c)]이다. 이 경우 제3고조파의 주파수가 기본파의 세 배이므로 같은 시간 이동에 상응하는 위상은 세 배가 된다. 즉 <$\phi_3 = 3\phi_1$>으로, 각 고조파가 그 주파수에 비례하는 위상각만큼 달라지면 파형이 그대로 유지된다.
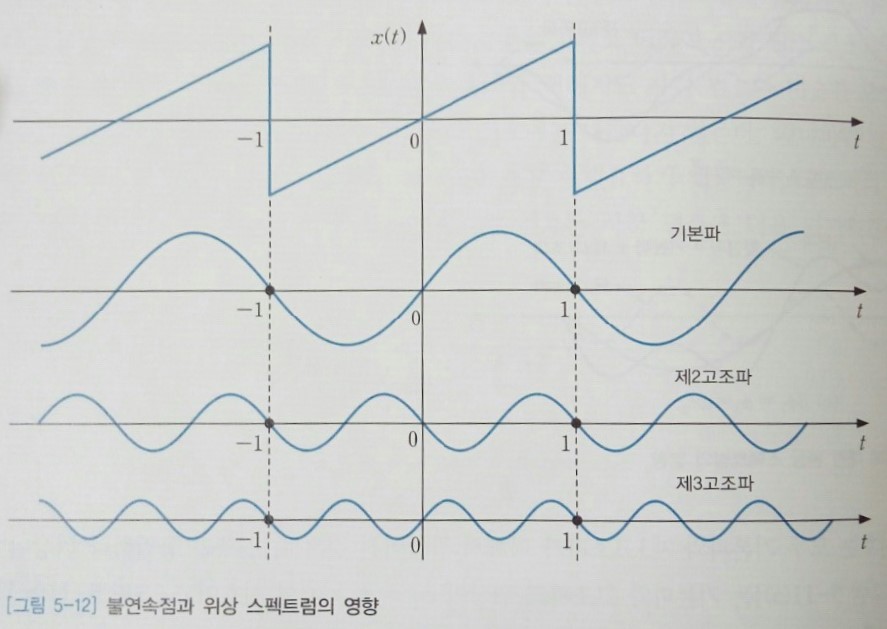
위상 스펙트럼의 또 다른 중요성은 불연속점과 같은 급격한 변화가 있는 신호를 통해 살펴볼 수 있다. 불연속점에서의 순간적인 변화를 만들어내기 위해서는 스펙트럼에 포함된 모든 (또는 대부분의) 고조파 성분이 불연속점 직전에서 같은 부호를 가져야 하며, 불연속점 직후에서 반대 부호를 가져야 한다. 다시 말해, 불연속점에서 모든 고조파 성분이 동일한 부호 변화를 보이며, 0점을 통과하도록 위상이 일치해야 한다. 이렇게 하면 합성된 신호의 불연속점에서는 날카로운 변화가 생기게 된다. 불연속점을 갖는 어떠한 신호의 파형에 대해서도 이러한 관계는 성립한다.
하나의 예로 [그림 5-12]의 톱니파 신호를 살펴보자. 이 그림에는 톱니파 신호의 파형과 함께 이 신호를 푸리에 급수로 전개한 결과의 첫 세 성분이 그려져 있다. 모든 주파수 성분의 위상은 불연속 신호를 푸리에 급수로 전개한 결과의 첫 세 성분이 그려져 있다. 모든 주파수 성분의 위상은 불연속 점인 <$t = \pm 1$>직전에는 모든 성분이 양이고 그 직후에는 음이 되도록 결정된다. 모든 고조파에서 일어나는 이러한 부호 변화가 더해져서 불연속점이 형성되는 것이다. <$t = 0$>에서 모든 고조파의 값은 0이 되지만 전후의 부호 변화가 일치하지는 않음을 볼 수 있다. 만약 위상 스펙트럼에 대한 조건이 맞지 않으면 모서리가 깎여나가고 퍼진 파형을 얻게 될 것이다.
이상의 논의에서 보았듯이, 신호를 합성할 때 위상 스펙트럼도 진폭 스펙트럼만큼 중요하다. 고조파의 진폭과 위상을 함께 적절히 조합해야 임의의 주기 신호 <$x(t)$>를 합성할 수 있으며, 이 고유한 조합이 바로 푸리에 스펙트럼Fourier Spectrum 이다.
푸리에 변환
세상에는 주기 신호보다 비주기 신호가 훨씬 많다. 따라서 비주기 신호에 대해서도 주파수 영역으로 변환할 수 있는 도구가 필요하다. 이때 가능하다면 논리적 일관성을 위해 이 도구가 푸리에 급수와 동일한 이론적 배경을 가지는 것이 바람직할 것이다.
푸리에 변환의 개요
푸리에 급수는 그 대상이 주기 신호에 한정되므로 더 폭넓게 비주기 신호에도 적용할 수 있는 주파수 영역 변환 도구를 찾아야만 한다. 하나의 방편으로 비주기 신호를 주기 <$T = \infty$>인 주기 신호로 간주해 푸리에 급수를 확장해 볼 수 있을 것이다.
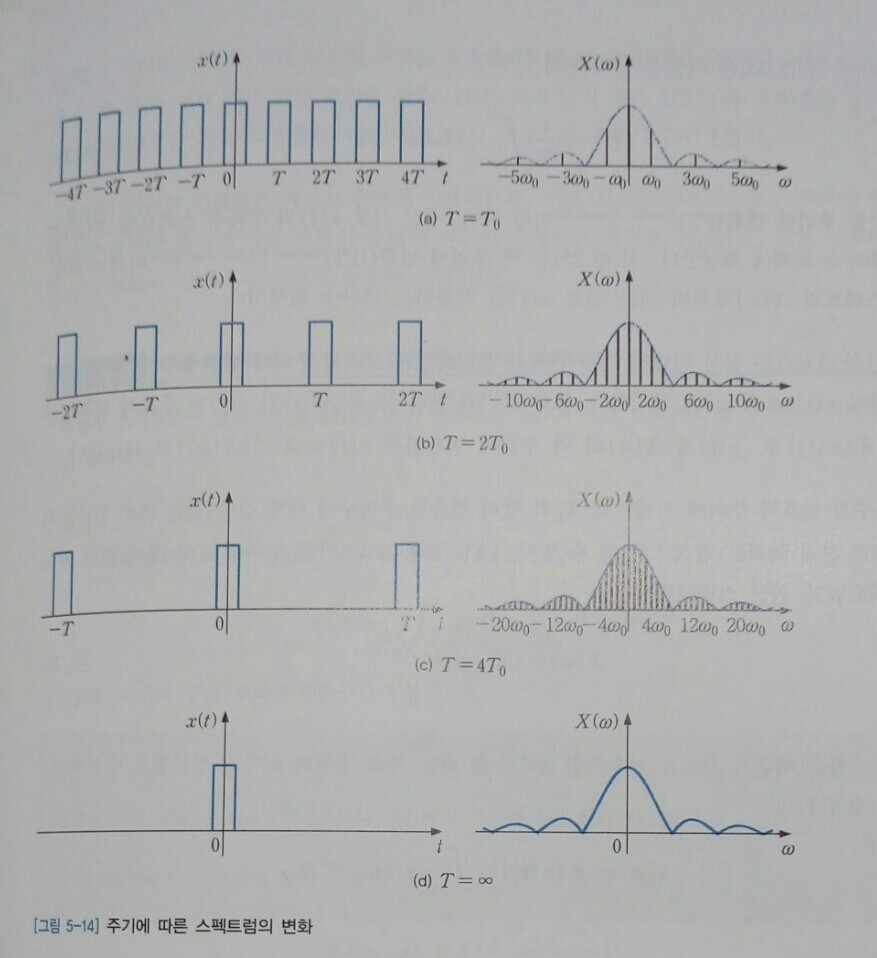
이에 앞서 먼저 주기 신호의 주기를 점점 크게 하면 어떤 현상이 생기는지 [그림 5-14]의 사각 펄스 주기 신호를 가지고 살펴보자.
주기 신호는 기본 주파수 <$\omega_0$>의 정수배인 주파수 성분만 존재하기 때문에 <$\omega_0$>의 간격으로 늘어선 선 스펙트럼으로 나타난다. 그런데 <$\omega_0$>는 주기 T에 반비례하므로, 주기 <$T$>를 크게 할 수록 <$\omega_0$>는 점점 작아져서 선 스펙트럼의 배열 간격이 점점 줄어들어 조밀해진다.
[그림 5-14]를 보면, 신호의 주기가 두 배가 되면선 스펙트럼의 배열 간격이 반으로 줄어들어 스펙트럼이 빽빽해진다([그림 5-14(b)]). 주기를 크게 할수록 이러한 현상은 더욱 심해지고([그림 5-14(c)]), 극단적으로 주기가 무한대이면, 즉 <$T \longrightarrow \infty$>의 극한을 취하면 <$\omega_0 \longrightarrow 0$>이 되어 스펙트럼이 연속적으로 이어지는 형태가 된다([그림 5-14(d)]). 이러한 개념에 대한 수학적 접근을 위해 푸리에 급수를 나타내는 식 (5.11)을 다시 쓰면 다음과 같다.
$$x(t) = \sum_{k = - \infty}^{\infty}X_k e^{jk\omega_0 t} = \sum_{k = - \infty}^{\infty} \left ( {\omega_0 \over 2\pi} \int_{-{T \over 2}}^{T \over 2} x(t)e^{-jk\omega_0 t} dt \right )e^{-jk\omega_0 t} \qquad \cdots \ (5.22)$$
<$T \longrightarrow \infty$>의 극한을 취하면 <$\omega_0 = {2\pi \over T}$>는 무한소가 되므로 <$\omega_0$>는 <$d\omega$>로, <$k\omega_0$>는 연속 변수 <$\omega$>로, 총합은 적분으로 바뀌어 식 (5.22)는 다음과 같이 바뀐다.
$$x(t) = \int_{\infty}^{\infty} \left [ {d\omega \over 2\pi} \int_{\infty}^{\infty}x(t)e^{-j\omega t}dt \right ] e^{j\omega t} \\ \qquad = {1 \over 2\pi}\int_{\infty}^{\infty} \left [ \int_{\infty}^{\infty}x(t)e^{-j\omega t}dt \right ]e^{-j\omega t}d\omega \qquad \cdots \ (5.23)$$
식 (5.23)의 두 번째 등식의 대괄호 안의 적분 항은 <$\omega$>의 함수이므로, 이를 다음과 같이
$$X(\omega ) = \int_{\infty}^{\infty} x(t)e^{-j\omega t}dt \qquad \cdots \ (5.24)$$
로 정의하면 식 (5.23)은 다음과 같이 된다.
$$x(t) = {1 \over 2\pi}\int_{\infty}^{\infty}x(t)e^{j\omega t}d\omega \qquad \cdots \ (5.25) $$
식 (5.24)를 푸리에 변환(FT)Fourier Transform이라 하며, 시간함수 <$x(t)$>의 주파수 스펙트럼 <$X(\omega )$>를 구하는 주파수 분해에 해당한다. 식 (5.25)는 역 푸리에 변환(IFT)Inverse Fourier Transform이라고 하며, 주파수 스펙트럼 <$X(\omega )$>로부터 시간신호 <$x(t)$>를 재현하는 주파수 합성이다.
이때 <$x(t)$>와 <$X(\omega )$>는 항상 일대일 대응 관계가 성립하는 쌍으로서 푸리에 변환쌍Fourier Transform Pair이라고 하며 <$x(t) \iff X(\omega )$>로 표기한다. 또한 표기가 편리하도록 <$X(\omega )$>가 <$x(t)$>의 푸리에 변환임은 <$X(\omega ) = \mathcal{F}\{ x(t) \}$>로, 역 푸리에 변환임은 <$x(t) = \mathcal{F}^{-1} \{ X(\omega ) \}$>로 나타낸다.
<$X(\omega )$>는 주기 신호의 푸리에 스펙트럼 <$X_k$>와 달리 연속된 주파수에 대해 값을 갖는 복소 함수로서 식(5.26)과 같이 극좌표 형식으로 쓸 수 있다. <$|X(\omega )|$>와 <$\angle X(\omega )$>를 주파수 <$\omega$>에 대해 그린 것이 진폭 스펙트럼과 위상 스펙트럼이다.
$$X(\omega ) = |X(\omega )|e^{-j\angle X(\omega )} \qquad \cdots \ (5.26)$$
푸리에 변환은 비주기 신호를 연속적인 주파수를 갖는 복소 정현파 <$e^{j\omega t}$>의 성분별로 구분하여 표시한 것이다.
$$X(\omega ) = \mathcal{F}\{ x(t) \} = \int_{-\infty}^{\infty}x(t)e^{-j\omega t} dt$$
푸리에 변환도 푸리에 급수와 마찬가지로 수렴 조건을 만족하는 신호에 대해서만 변환할 수 있다. 푸리에 변환은 주기 <$T$>가 무한대인 푸리에 급수에 해당되므로 기존의 디리클레 조건에서 주기와 관련된 부분들이 바뀌게 된다. 이를 정리하면 다음과 같다.
- 전 시간 구군에 대해 <$x(t)$>는 절대 적분 가능해야 한다.
$$\int_{-\infty}^{\infty}|x(t)|dt\ < \ \infty \qquad \cdots \ (5.27)$$ - 어떤 유한한 시간 구간에서의 신호의 극대 극소점의 수는 유한해야 한다.
- 어떤 유한한 시간 구간에서 신호의 불연속점의 수는 유한해야 한다.
유한한 에너지를 갖는 에너지 신호는 항상 식 (5.27)의 절대 적분 가능 조건을 충족시킨다. 이와 달리 계단 신호나 주기 신호와 같이 무한한 에너지를 갖지만 전력이 유한한 전력신호는 식 (5.27)을 충족시키지 못한다.
그렇지만 이러한 신호들은 폭넓고 흔하게 사용되므로, 전력 신호는 이론적으로는 푸리에 변환이 존재하지 않지만 필요에 의해 특별히 푸리에 변환이 존재하는 것으로 취급한다. 전력 신호의 푸리에 변환은 주파수 영역에서 임펄스 함수를 포함한다.
주기 신호의 푸리에 변환
비주기 신호 <$x(t)$>의 푸리에 변환 <$X(\omega ) $>와 이 비주기 신호를 주기 <$T$>로 반복시켜 얻은 주기 신호 <$x_T (t)$>의 푸리에 변환 <$X_T (\omega )$>의 관계를 살펴보자.
푸리에 급수 표현을 이용하여 <$x_T (\omega )$>의 푸리에 변환을 구하면
$$X_T = \int_{-\infty}^{\infty} x_T (t)e^{-j\omega t} dt = \int_{-\infty}^{\infty}\left ( \sum_{k=-\infty}^{\infty} X_k e^{jk\omega _0 t} \right )e^{-j\omega t}dt \\ \qquad = \sum_{k=-\infty}^{\infty} X_k \int_{-\infty}^{\infty} \left ( e^{jk\omega _0 t} \right ) e^{-j\omega t}dt = 2\pi \sum_{k=-\infty}^{\infty}X_k \delta (\omega - k\omega_0) \qquad \cdots \ (5.31)$$
이다. 식 (5.31)로부터 주기 신호의 푸리에 변환은 기본 주파수의 정수배에 위치한 임펄스 함수들로 이루어져 있으며, 임펄스의 세기는 <$x_T (t)$>를 푸리에 급수로 전개했을 때 그 주파수의 푸리에 계수 <$X_k$>의 <$2\pi$>배로 주어짐을 알 수 있다.
그런데 한 주기 구간 동안 <$x_T (t)$>는 <$x(t)$>와 같고, 그 외의 구간에서 <$x(t) = 0$>이라는 사실을 이용하면, 주기 신호의 푸리에 계수 <$X_k$>는 다음과 같이 된다.
$$X_k = {1 \over T}\int_{T}x_T (t)e^{-jk\omega _0 t}dt = {1 \over T}\int_{-\infty}^{\infty}x(t) e^{-jk\omega t}dt = {1 \over T}X(k\omega_0 ) \qquad \cdots \ (5.32)$$
식 (5.32)를 식(5.31)에 대입하여 정리하면 다음과 같다.
$$X_T (\omega ) = {2\pi \over T}\sum_{k=-\infty}^{\infty}X(k\omega _0 ) \delta (\omega - k\omega_0 ) = \omega_0 \sum_{k=-\infty}^{\infty}X(k\omega _0 ) \delta (\omega - k\omega_0 ) \qquad \cdots \ (5.33)$$
식(5.32)에서 보면, 주기 신호의 푸리에 급수의 계수 <$X_k$>는 비주기 신호의 푸리에 변환 <$X(\omega )$>를 크기를 <$1 \over T$>배하여 기본 주파수의 정수배, 즉 고조파 주파수 <$k\omega_0$>에서 샘플링한 값이다. 또한 식 (5.33)으로부터 주기 신호의 푸리에 변환은 비주기 신호의 푸리에 변환 <$X(\omega )$>를 고조파 주파수 <$k\omega_0$>에서 임펄스 샘플링한 것으로, 임펄스의 세기는 해당 주파수의 비주기 신호 푸리에 변환 값 <$X(k\omega _0 )$>에 주기 신호의 기본 주파수 <$\omega_0$>를 곱한 값이다.
이상의 결과로부터, 주기 신호를 푸리에 급수로 나타내든 푸리에 변환으로 나타내든 간에 주기 신호의 스펙트럼은 같은 파형을 가진 비주기 신호의 푸리에 변환을 샘플링한 이산 함수가 되며, 선 스펙트럼의 간격은 기본 주파수 <$\omega_0$>로 주어진다는 결론을 얻을 수 있다. 이는 [그림 5-14]와도 일치한다.
푸리에 변환의 성질
[변조]
어떤 신호에 다른 신호를 곱하여 새로운 신호를 만들어 내는 동작을 변조modulation라고 하는데, 가장 기본적인 변조 방식이 [그림 5-16]에 나타낸 진폭변조(AM)Amplitude Modulation이다. 진폭 변조는 신호 <$x(t)$>에 정현파 <$cos\omega _0 t$>를 곱하여 정현파의 진폭을 변조시키는데, 정현파<$cos\omega _0 t$>는 신호 <$x(t)$>를 담아 나르는 역할을 하기 때문에 반송파carrier라 하며, 주파수 <$\omega_0$>를 반송 주파수carrier frequency라고 한다. 정현파<$cos\omega _0 t$>로 진폭 변조된 신호의 푸리에 변환을 구하면
$$\mathcal{F} \left\{x(t)cos\omega_0 t \right\} = {1 \over 2}\int_{-\infty}^{\infty}\left [ x(t)(e^{-j\omega_0 t}) \right ] e^{-j\omega t}dt \\ \qquad = {1 \over 2}\left (\int_{-\infty}^{\infty}x(t)e^{-j(\omega - \omega_0)t}dt + \int_{-\infty}^{\infty}x(t)e^{-j(\omega + \omega_0)t}dt \right ) \qquad \cdots \ (5.36) \\ \qquad = {1 \over 2} \left (X(\omega - \omega_0 ) + X(\omega + \omega_0 ) \right )$$
이다. 식 (5.36)은 <$x(t)$>에 주파수 <$\omega_0$>인 정현파를 곱하면 스펙트럼 <$X(\omega )$>가 <$\pm \omega_0$>만큼 이동됨을 보여준다. 이처럼 진폭 변조는 신호의 주파수 대역 이동에 이용한다. 예를들어, 모든 라디오 방송국이 동시에 음성 신호들을 방송한다면, 신호 상호 간에 간섭으로 수신기는 그 방송들을 분리할 수 없을 것이다. 그러나 각 라디오 방송국이 서로 다른 반송 주파수를 할당받아 주파수를 이동한 (변조된) 신호를 전송하게 되면, 라디오 수신기는 원하는 방송의 주파수 대역에 동조하여 방송을 수신할 수 있게 된다.
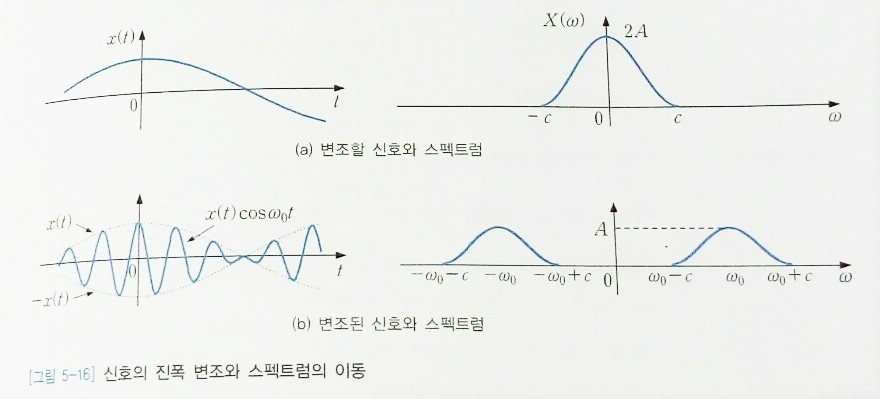
변조를 사용하는 또 다른 예로는 원래의 기저대역baseband 신호가 전송채널(안테나, 동축케이블, 광섬유 등)에 전송하기에 적합하지 않는 경우를 들 수 있다. 예를 들어, 음성 신호는 주파수대가 너무 낮아서, 즉 파장이 너무 길어서 이를 전파하려면 큰 안테나가 필요하다. 이 문제를 해결하려면 변조에 의해 (파장이 짧은) 높은 주파수 영역으로 스펙트럼을 이동시키면 된다.
이외에도 유용한 성질들이 많이 있으나, 아래 표에 푸리에 변환의 주요 성질들을 정리하여 나타내었다.
