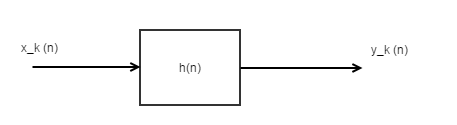
System의 분류
공학적인 입장에서 Causal & Stable 이라는 요구조건은 반드시 필요한 조건이다!
-
Dynamic
- Linear
- Time Invariant
- Causal
미래의 입력에 영향을 받지 않는 시스템 - Stable
예제
<$y_1 (n) = x^2 (n)$>
- Linear 여부: 제곱이 있으므로 Linear하다.
- Time Invariant 여부: TI 하다.
- Causal 하다.
<$y_2 (n) = ax(n) + b$>
- Linear 여부: non-linear system이다.
<$T(0) = 0$> 임을 만족하지 않음.
<$y_3 (n) = n \cdot x(n)$>
- Linear 여부: Linear 이다.
T(0) = 0 이지만 이 조건만으로는 Linear 여부를 확신할 수 없음
<$x_1 \longrightarrow y_1 = nx_1$>
<$x_2 \longrightarrow y_2 = nx_2$>
<$ax_1 + bx_2 \longrightarrow n(ax_1 + bx_2 ) = a \cdot nx_1 + b \cdot nx_2 = ay_1 + by_2$>
즉, 선형 조합으로 입력되었을 때 동일한 형태로(=각 신호에 대한 출력신호에 동일한) 출력신호가 나타나게 되면 Linear 하다.
Super Position 특성을 만족한다. - Time-Invariant 여부: Time Variant 시스템이다.
<$T(x(n)) = nx(n)$> 이라 할때, <$T(x(n-t)) = y(n, k) = nx(n-k)$> 이 된다.
하지만 위 식에 <$n-k$>를 대입한 결과가 <$y(n-k) = (n-k) \cdot x(n-k)$> 이므로 위 식과 다르다. 따라서 본 시스템은 Time Variant 시스템이 된다.
<$y_5 (n) = x(n^2 )$>
- Linear 여부: Linear system이다.
- Time Invariant 여부: Time Invariant 이다
- Causal 여부: non-causal 이다.
<$y_5(-1) = x(1)$>
정리
- 종속변수(<$x(n)$>)에 대한 임의의 함수의 형태로 연산이 주어졌을 때, 그 시스템은 비선형 시스템이다.
ex) <$y(n) = e^{x(n)}$>, <$\sqrt{x(n)}$> 등등 - Time-Variant와 Time-Invariant를 구분하는 방법은 까다롭다.
<$y(n) = n \cdot x(n)$> 이 있을 때,- Time-Varing System: 종속변수(<$x(n)$>) 앞에 붙는 임의의 계수(<$n$>: coefficient)의 값이 n에 대한 함수로 주어졌을 때, 즉 상수가 아닐 때
<$y_8 (n) = x(-n)$> (<$-n$> : scaling / folding)
- Time-Varing System: 종속변수(<$x(n)$>) 앞에 붙는 임의의 계수(<$n$>: coefficient)의 값이 n에 대한 함수로 주어졌을 때, 즉 상수가 아닐 때
- Causal System을 구분하는 방법(쉬움)
특성방정식에 <$n = \pm 1$>을 대입하여 현재의 출력이 미래의 입력에 영향을 받는지만 확인하면 됨.
시스템간의 연결 (Interconnection of System)
이산시간 시스템을 서로 연결한다고 했을 때, 어떻게 할까?
직렬연결 (Cascade Connection)
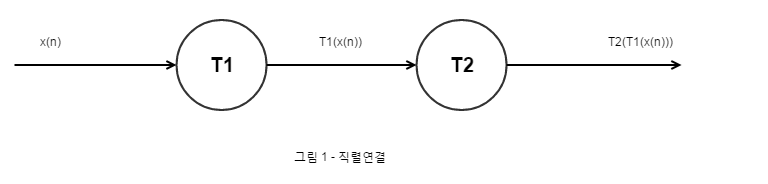
의문점1: 만약에 T1과 T2라는 시스템의 순서를 바꾸고자 한다면 어떻게 해야될까?
과연 그림 1의 출력신호와 그림 2의 출력신호가 같을까? 다르다.
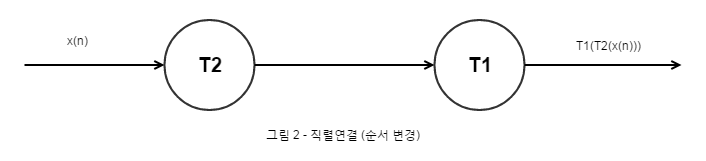
두 DT 시스템을 직렬연결하였을 때, 순서를 바꾸면 그 최종 출력신호는 달라진다. 하지만, T1과 T2가 특정한 조건을 만족하면 둘의 순서를 바꾸어도 출력이 바뀌지 않는 상황이 있을 수 있을 것이다. 이렇게, 두 시스템의 순서를 바꾸어도 출력이 바뀌지 않는 시스템을 LTI(Linear Time Invariant) System 이라 부른다.
병렬연결 (Parallel Connection)
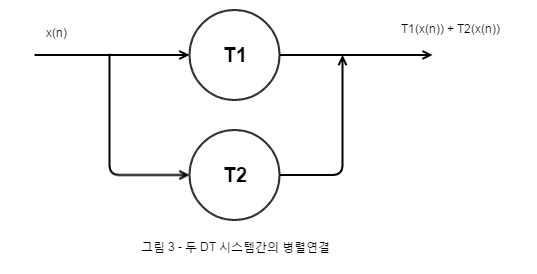
Analysis of LTI Systems
왜 System을 분석(해석)할까?
- 어떤 출력이 나올지 알고싶다.
- 어떤 입력에 의해서 어떤 출력이 나타나는지 알고싶다.(예측하고 싶다)
- 우리가 원하는 입력을 통해 원하는 출력을 만들고 싶으면, 분석이 필요하다.
일반적으로 LTI System은 아래와 같은 System 방정식이 주어진다.(차분방정식)
$$y(n) + \sum_{k=1}^{N}a_k y(n-k) = \sum_{k=1}^{M}b_k x(n-k)$$
- 종속변수인 <$y(n)$>에 대한 연산은 존재하지 않음을 알 수 있다. (Linear)
- 종속변수에 임의의 상수를 곱하는 연산만 존재한다. (Time Invariant)
- 계수가 모두 상수이다. (Time Invariant)
아래와 같은 system이 있다고 하자,
$$y(n) = {1 \over 2} y(n-1) + {1 \over 3} \left ( x(n) + x(n-1) \right ),\ x(n) = u(n),\ y(0) = 0$$
위 시스템에서 <$n = 1$>이면, 아래와 같이 system을 해석할 수 있을 것이다.
<$y(1) = {1 \over 2}y(0) + {1 \over 3} \left ( x(1) + x (0) \right )$>
<$y(1000)$>을 구하라고 한다면, <$y(1)$>부터 계산하는 사람도 있을 것이다. 하지만 이런 경우에는 정형화된 해석방법이 있지 않을까?
미분방정식과는 다르게, 차분방정식에서는 정형화된 솔루션기법은 별로 큰 의미를 갖지 않는다.
차분방정식을 푸는 방법 이외에 시스템을 이해하는 방법은 없을까? 차분방정식을 푸는 방법(=time-domain analysis)은 일반적으로 효율적이지 못하다.
time-domain analysis
약자: TD (Time-domain)
차분방정식을 직접 풀어서 해석하는 방법. 효율적이지 못하다.
Frequency-domain analysis
약자: FD(Frequency-domain)
엄밀한 의미로 표현하자면 Frequency-domain 이라는 용어 보다는 Transform-domain이 적합할 수 있다.
|
Transform-domain의 기본적인 개념은, 입력신호를 우리가 다루기 굉장히 편리한 신호의 선형 조합으로 표현하겠다는 것이다. $$x(n) = \sum_{k} c_k x_k (n)$$ 위 식은 Elementary Signal(<$x_k (n)$>)의 선형 조합을 의미한다. 여기서 <$x_k (n)$>을 elementary(basis) signal 이라 부르는데, elementary signal(<$k$>가 정수인 집합)은 아래와 같이 두 가지 요구조건이 있다.
<$h(n)$>이라는 Impulse Response를 가지고 있는 LTI System에서 <$x_k (n)$>이 complexity exponential의 형태로 입력되었을 때, 출력신호는 동일한 complexity exponential 신호가 그대로 남아있고 단지 그 크기와 위상값만 변경된다. 즉, $$y_k (n) = H(k{\omega}_0) \cdot x_k (n)$$ 이다. 여기서 <$H(k{\omega}_0)$>(frequency response)는 복소수 값이다. 이 값 때문에 크기와 위상이 변경된다.
|
Response of LTI System
LTI System에서 임의의 입력<$x(n)$>이 주어졌을 때, 그때의 출력신호는 무엇이 될 것인가를 알아보자.
만약에 <$T$>라는 연산으로 표현되는 임의의 LTI System이 있을 때, 입력 <$x(n)$>에 대한 출력 <$y(n)$>은 어떻게 될까?
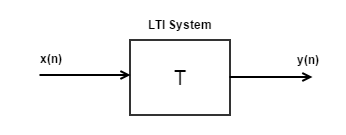
위 문제를 해결하기 위한 접근방법으로는 두 가지가 있다.
time-domain analysis
LTI System에서의 입력은
$$x(n) = \sum_{k = - \infty}^{\infty}x(k)\delta (n-k)$$
으로 표현할 수 있으며, 이를 Impulse function의 shifting property라 말한다. 이 <$x(n)$>이 입력되었을 때, <$y(n)$>의 경우는 아래와 같이 표현될 수 있다.
$$y(n) = T \left (x(n) \right ) = T \left ( \sum_{k = - \infty}^{\infty}x(k)\delta (n-k) \right )$$
여기서 <$T$>는 LTI System 이고, Linear이기 때문에, Superposition의 원칙에 따라서 <$T$>라는 연산과, <$\sum$> 나아가서는 <$T$>라는 연산과 상수값(<$x(k)$>)의 순서를 바꾸어 주어도 된다. 따라서 위 식을 계속 전개하면,
$$= \sum_{k} x(k) \cdot T \left ( \delta (n-k) \right )$$
이고, 초기조건이 0(=system이 reset)인 상태에서의 출력을 <$T \left ( \delta (n) \right ) = h(n)$>이라 정의 해 보자.
|
일반적으로 DSP 영역에서는 초기조건이 0(=system이 reset)이라 가정한 상태에서 impulse 입력이 주어졌을 때의 출력을 <$T \left ( \delta (n) \right ) = h(n)$> 으로 정의한다. 여기서 <$h(n)$>을 Impulse Response 라고 부른다. |
$$\therefore y(n) = \sum_{k = - \infty}^{\infty} x(k)h(n-k) = x(n) * h(n)$$
에 의해서 정의된다. 위 표현(<$x(n) * h(n)$>)을 Convolution(합성곱) 이라 정의한다. 이 수식을 사용해서 임의의 입력 <$x(n)$>이 주어지고, 우리가 그 시스템의 impulse response <$h(n)$>을 알 때, 그 시스템의 출력신호<$y(n)$>을 구할 수 있다.
|
Convolution(합성곱) 연산을 어떻게 처리해 주어야 할까? 위 Convolution을 정의하는 식에서 <$n$>은 Time Variable이다. 그리고 출력을 구한다는 것은 <$y(n)$>이 0이 아닌 범위 내에서 모든 <$n$> 에 대해서 <$y(n)$>의 값을 계산해 주어야 한다는 것이다. 따라서 n의 범위는 <$- \infty < n < \infty $>가 된다. 어떤 고정된 시간(fixed time)에 대해 <$n = n_0$> convolution 값을 구한다고 생각한다고 생각해 보자. 이 경우 출력인 <$y(n_0 )$>는 $$y(n_0 ) = \sum_{k= - \infty}^{\infty }x(k)h(n_0 -k)$$ 가 된다. 위 식에서 <$n_0$>는 상수이므로, 우리는 <$k$>라는 독립변수를 기준으로 해석해야 한다는 것을 알 수 있다. 이 때, <$h(n_0 -k)$>는 두 가지 형태로 생각될 수 있다.
따라서,위 수식을 기반으로 해서 특정한 시점인 <$n_0$>에서의 출력을 구하기 위해서는 첫번째, folding연산을 수행한다. <$h(k) \longrightarrow h(-k)$> 두번째, shift 연산을 수행한다. <$h(-k) \longrightarrow h(n_0 -k)$> 세번째, mult 연산을 수행한다. <$x(k) \cdot h(n_0 -k)$> 두개의 신호를 곱해준다는 것은, 모든 <$k$>의 범위(0, 1, 2...)에서 <$x(k)$>값과 <$h(n_0 -k)$>값을 곱해준다는 것을 의미한다. (하나의 sequence로 나타나게 된다.) 네번째, 모든 k에 대해서 더해준다. (addup, <$\sum$>) 기본적으로 Convolution 연산은, time이 고정된 경우에서 네가지 단계에 의해 특정 시점의 출력을 구할 수 있다. |
Convolution(합성곱)의 예
아래 그림과 같이 Impulse Response <$h(n)$>과 입력신호 <$x(n)$>이 주어진 경우, convolution 연산의 결과를 계산해 보자.
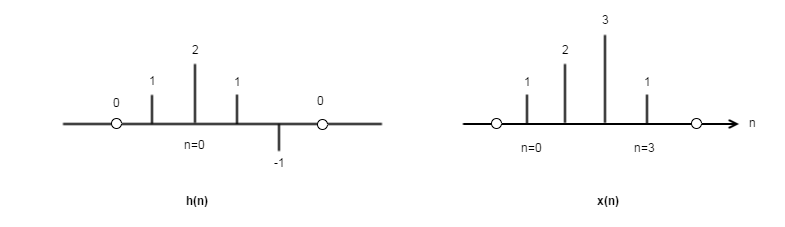
위 문제의 해법은 세 가지 방법이 있다. (Graphical Approach)
첫번째, <$n = 1$>로 고정된 경우,
- folding: <$n=1$> 인 지점을 기준으로 좌우 대칭한다.
- 오른쪽으로 <$n_0$>만큼 shifting 한다.
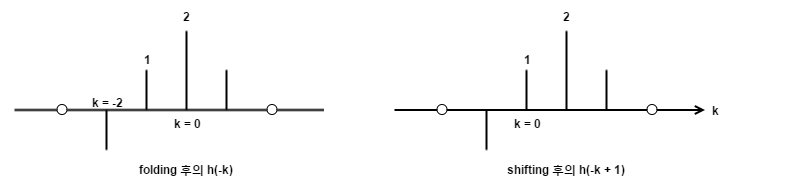
-
mult(곱) 연산을 수행한다.
<$x(n)$>의 각 n의 index에 해당하는 값과, <$h(-k + 1)$>의 각 k의 index에 해당하는 값과 곱해주면 된다.
(0이 아닌 값을 가지는 범위 내에서만 구해주면 된다.)n / k의 index <$x(n)$> <$h(-k+1)$> Convolution 결과 -1 0 -1 0 0 1 1 1 1 2 2 4 2 3 1 3 3 1 0 0 합계 8
참고로 위 식에서 <$y=0$>를 만족하는 n의 범위는 다음과 같다.
$$y=0, \ \begin {cases} n \le -2 \\ n \ge 6 \end {cases}$$
|
Graphical Approach
|
두번째, Table 구성을 통한 활용기법
| k | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | y(n) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| <$x(k)$> | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 1 | 0 | 0 | |
| <$h(k)$> | 0 | 0 | 0 | 1 | 2 | 1 | -1 | 0 | 0 | 0 | |
| <$n=0$>일때, <$h(-k)$> (folding) |
0 | 0 | -1 | 1 | 2 | 1 | 0 | 0 | 0 | 0 | <$2+2 = 4$> |
| <$n=-1$>일때, <$h(-k-1)$> (좌측 shift) |
0 | -1 | 1 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | <$1$> |
| <$n=1$>일때, <$h(-k+1)$> (우측 shift) |
0 | 0 | 0 | -1 | 1 | 2 | 1 | 0 | 0 | 0 | <$1+4+3 = 8$> |
| <$n=2$>일때, <$h(-k+2)$> (우측 shift) |
0 | 0 | 0 | 0 | -1 | 1 | 2 | 1 | 0 | 0 | <$-1+2+6+1=8$> |
세 번째, 아래와 같이 표현하면 covolution을 쉽게 구할 수 있다.
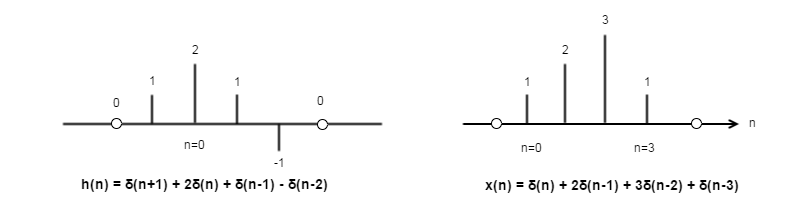
위 식을 Table로 표현하면, Convolution 연산을 쉽게 계산할 수 있다.
| n=-1 | n=0 | n=1 | n=2 | n=3 | n=4 | n=5 | 비고 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | -1 | <$x(n) = \delta (n)$>이 입력되었을 때, <$h(n)$>식에서 <$\delta$> 앞 계수들 |
|||
| 2 | 4 | 2 | -2 | <$x(n) = 2\delta (n-1)$>이 입력되었을 때, 2를 곱하고, 1만큼 shift연산 |
|||
| 3 | 6 | 3 | -3 | <$x(n) = 3\delta (n-2)$>이 입력되었을 때, 3를 곱하고, 1만큼 shift연산 |
|||
| 1 | 2 | 1 | -1 | <$x(n) = \delta (n-3)$>이 입력되었을 때, 1을 곱하고, 3만큼 shift연산 |
|||
| 1 | 4 | 8 | 8 | 더해준다. |
|
Matlab에서의 Convolution 연산
다만, Matlab에서의 계산 결과 해석이 필요하다. |